https://www.acmicpc.net/problem/13907
13907번: 세금
첫 번째 줄에 세 정수 N (2 ≤ N ≤ 1,000), M (1 ≤ M ≤ 30,000), K (0 ≤ K ≤ 30,000)가 주어진다. 각각 도시의 수, 도로의 수, 세금 인상 횟수를 의미한다. 두 번째 줄에는 두 정수 S와 D (1 ≤ S, D ≤ N, S ≠ D
www.acmicpc.net
주언이는 경제학을 배워 행상인이 되었다. 두 도시를 오가며 장사를 하는데, 통행료의 합이 가장 적은 경로로 이동하려 한다. 도시들은 양방향 도로로 연결되어있으며, 도로마다 통행료가 존재한다.
그런데 정부는 세금 인상안을 발표하였다. 세금을 한 번에 올리면 문제가 발생할 수 있으므로 여러 단계에 걸쳐서 올린다고 한다. 세금이 A만큼 오르면 모든 도로의 통행료가 각각 A만큼 오르게 된다. 세금이 오르게 되면 주언이가 내야 하는 통행료가 변할 수 있다.
주언이를 도와 초기의 최소 통행료와 세금이 오를 때마다의 최소 통행료를 구하시오.
-------------------------------------------------------------------------
N<=1000 M<=30000 K<30000이므로
최소거리를 구하는데 사용되는 다익스트라를 30000번 사용하면
O(30000 *log1000)*30000)이므로 당연히 시간초과가 난다.
기존 다익스트라가 경로에 상관없이 i 부터 j 까지 가는 최단 거리를 구했다면 이를 변형해서
DD[n][j] = n개의 도시를 거쳐서 j까지 가는 최단거리라고 규정해보자.
edge 또한 기존 (v,w)에서 (v,w,n) (도착점 번호, 경로의 길이, 거쳐간 도시수)로 바뀐다.
이 두가지로 변형된 다익스트라는 기존 다익스트라와 다음과 같이 다르다.
1. 기존의 다익스트라는 거쳐간 도시에 상관없이 최소거리인지만 체크했다면, 변형된 다익스트라는 거쳐간 도시수를 포함하여 최소거리를 체크한다.
2. 단 도시수만 이용해서 다익스트라를 돌릴 경우 체크할 필요가 없는 간선들까지 모두 체크되므로 메모리초과가 난다. 그러므로 거쳐간 도시가 같은 경우 뿐만 아니라 작거나 같은 경우 수까지 모두 체크해준다.
※ 그 이유는 도시가 2개의 도시를 거쳐간 경우와 3개의 경우를 거쳐간 경우를 비교했을때
3개를 거쳐간 경우가 세금의 증가량이 더 크다(3개는 *3 이고 2개는 *2)이므로
그러므로 초기비용마저 3개인 경우가 더 크면 기울기가 3개인게 더 크므로 2개의 도시보다 무조건 클수밖에없다.
예제를 이용해서 설명하겠다.
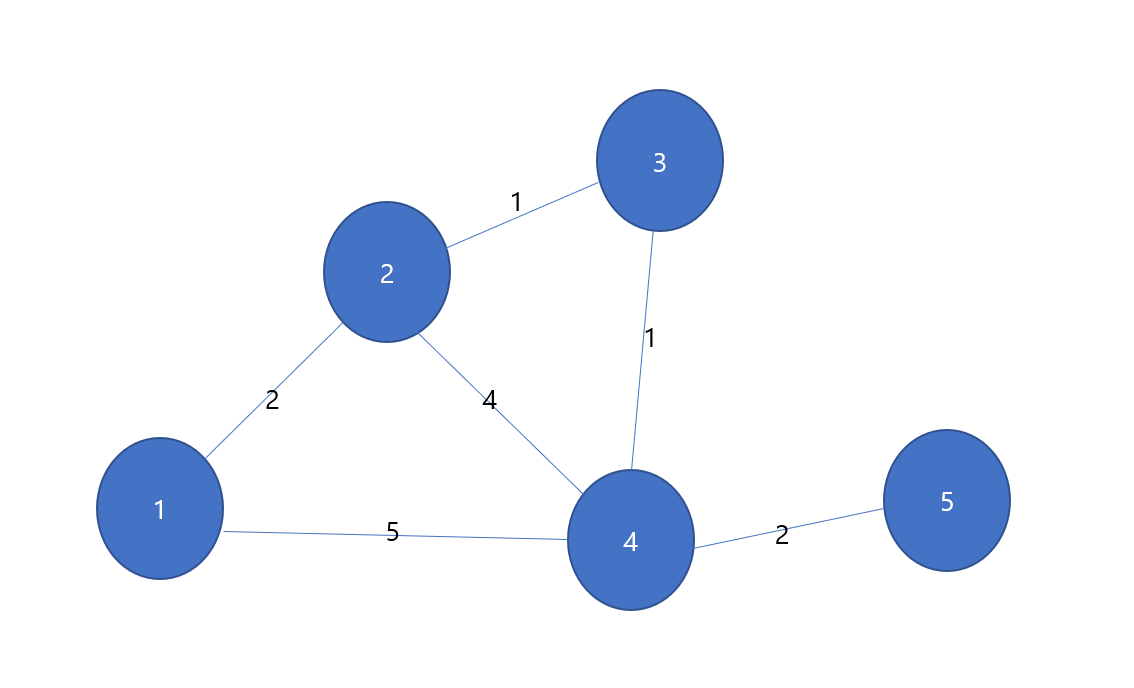
1)
| 1) | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | INF | INF | INF | INF |
| 1 | INF | INF | INF | INF | INF |
| 2 | INF | INF | INF | INF | INF |
| 3 | INF | INF | INF | INF | INF |
| 4 | INF | INF | INF | INF | INF |
초기 값은 모두 시작점 빼고 모두 INF이다.
2)
| 2) | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | INF | INF | INF | INF |
| 1 | INF | 2 | INF | 5 | INF |
| 2 | INF | INF | INF | INF | INF |
| 3 | INF | INF | INF | INF | INF |
| 4 | INF | INF | INF | INF | INF |
1에서 (2,2,0) (4,5,0) 이 추가된다. DD[1][2] DD[1][4] 가 각각 2, 5 로 바뀐다.
3)
| 3) | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | INF | INF | INF | INF |
| 1 | INF | 2 | INF | 5 | INF |
| 2 | INF | INF | 3 | INF | INF |
| 3 | INF | INF | INF | INF | INF |
| 4 | INF | INF | INF | INF | INF |
가장 작은 edge가 (2,2,0)가 pop되고
(3,1,1) (4,4,1) (1,2,1)이 테스트된다.
D[2][3] = INF 이므로 (3,1,1)은 통과된다.
D[2][4] = INF이지만 D[1][4]가 5다. 그러므로 5 < 2 + 4 =6 이므로 이 경로는 절대 최소경로가 될수없으므로 통과 X
D[2][1] = INF 이지만 D[0][1] 가 0 이다. 그러므로 0 < 2+2 이므로 이 경로 또한 절대 최소경로가 될수없다.
4)
| 4) | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | INF | INF | INF | INF |
| 1 | INF | 2 | INF | 5 | INF |
| 2 | INF | INF | 3 | INF | INF |
| 3 | INF | INF | INF | 4 | INF |
| 4 | INF | INF | INF | INF | INF |
가장 작은 Edge인 (3,1,2)이 pop되고
(2,1,2) (4,1,2)가 테스트 된다.
D[3][2] = INF이지만 D[2][1] =2이다. 그러므로 2< 3+1 이므로 이 경로는 최소경로가 될 수 없다.
D[3][4] = INF이고 D[1][4] = 5이다. 5< D[2][3](3) + dist[3][4](1) 이므로 이 경로는 최소경로가 될 수 있다.
5)
| 5) | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | INF | INF | INF | INF |
| 1 | INF | 2 | INF | 5 | INF |
| 2 | INF | INF | 3 | INF | INF |
| 3 | INF | INF | INF | 4 | INF |
| 4 | INF | INF | INF | INF | 6 |
가장 작은 Edge (4,1,3)이 pop된다.
4에서 파생된 Edge는 3개다.
(3,1,4)의 경우 D[4][3] = INF 이지만 D[2][3]= 2이므로 최소경로가 될수없음
(1,5,1)의 경우 D[2][1] = INF 이지만 D[0][1] = 0 이므로 최소경로가 될수없음
(5,2,3)의 경우 D[4][4] = INF 이고 나머지도 모두 INF 이므로 최소경로가 될수있음 4+2 =6
6)
| 6) | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | INF | INF | INF | INF |
| 1 | INF | 2 | INF | 5 | INF |
| 2 | INF | INF | 3 | INF | INF |
| 3 | INF | INF | INF | 4 | INF |
| 4 | INF | INF | INF | INF | 6 |
가장 작은 Edge인 (5,2,4)가 pop된다.
5에서 파생된 Edge는 1개다.
(4,2,5) 의경우 5가 노드갯수보다 크보다 작으므로 경로가 될수없다.(사이클 존재)
7)
| 7) | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | INF | INF | INF | INF |
| 1 | INF | 2 | INF | 5 | 7 |
| 2 | INF | INF | 3 | INF | INF |
| 3 | INF | INF | INF | 4 | INF |
| 4 | INF | INF | INF | INF | 6 |
가장 작은 Edge인 (4,4,1)이 pop된다.
4에서 파상된 Edge는 4개지만
(5,2,1)를 제외한 나머지 Edge들은 위와 같은 이유로 최소경로가 될수없다.
(5,2,1)를 이용한 최소 경로는 5+2 =7이다.
이로써 모든 다익스트라가 끝난다. 위 테이블을 이용하여 답만 구하면 끝이다.
package 백준;
import java.util.*;
import java.io.*;
public class 세금 {
public static class MyScanner {
BufferedReader bf;
StringTokenizer st;
MyScanner() {
bf = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while (st == null || !st.hasMoreTokens()) {
try {
st = new StringTokenizer(bf.readLine());
} catch (Exception e) {
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt() {
return Integer.parseInt(next());
}
public long nextLong() {
return Long.parseLong(next());
}
}
public static void main(String[] args) {
MyScanner sc = new MyScanner();
int N = sc.nextInt();
int M = sc.nextInt();
int K = sc.nextInt();
int S = sc.nextInt();
int D = sc.nextInt();
ArrayList <int[]> edges[] = new ArrayList[N+1];
for(int i = 0;i<=N;i++) {
edges[i] = new ArrayList<int[]>();
}
int DD[][] = new int[N+2][N+2];
int INF = 987654321;
int inc[] = new int[K];
for(int i =0 ;i<=N+1;i++)
Arrays.fill(DD[i], INF);
for(int i =0 ;i<M;i++) {
int x= sc.nextInt();
int y= sc.nextInt();
int z=sc.nextInt();
edges[x].add(new int[] {y,z});
edges[y].add(new int[] {x,z});
}
DD[0][S] = 0;
PriorityQueue <int[]> pq = new PriorityQueue <int[]>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
pq.add(new int[] {S,0,0});
while(!pq.isEmpty()) { // new 다익스트라 DD[i][j] = i개의 도로를 거쳐서 j로 갔을때의 최소거리
int now[] = pq.poll();
int u = now[0];
int w = now[1];
int n = now[2];
if(n>=N) continue;
if(w>DD[n][u]) continue;
fr:for(int i=0;i<edges[u].size();i++) {
int v = edges[u].get(i)[0];
int ww = edges[u].get(i)[1];
for(int j = 0 ;j <= n;j++) {
if(DD[n][u]+ww> DD[j][v]) continue fr; //i개 도로보다 적게 간 경우수중에 지금 경로보다 작으면 최소경로가 절대 될수가없다. 세금올려도 내증가분이 더 많기 때문
}
if(DD[n+1][v]>DD[n][u] + ww) {
DD[n+1][v] = DD[n][u] + ww;
pq.add(new int[] {v,ww,n+1});
}
}
}
for(int i =1 ;i <N;i++) {
for(int j =1;j<=N;j++) {
//System.out.print(DD[i][j]+ " ");
}
//System.out.println();
}
int k = 0;
int answer = INF;
for(int j=1;j<=N;j++) {
answer = Math.min(j*k+DD[j][D], answer);
}
System.out.println(answer);
for(int i =0 ;i <K;i++) {
inc[i] = sc.nextInt();
k+=inc[i];
answer = INF;
for(int j=1;j<=N;j++) {
answer = Math.min(j*k+DD[j][D], answer);
}
System.out.println(answer);
}
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 16228 GCC의 유산 (0) | 2020.05.09 |
|---|---|
| 백준 15927 회문은 회문아니야!! (0) | 2020.05.07 |
| 백준 문자열제곱 4354 (0) | 2020.05.02 |
| 백준 15824 너 봄 캡사이신이 맛있단다. (0) | 2020.04.29 |
| 백준 1669멍멍이 쓰다듬기 (0) | 2020.04.23 |